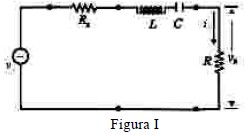
Um dos elementos mais importantes encontrados em um receptor de sinais de radiofreqüência é o filtro elétrico, que permite selecionar um sinal desejado entre os diversos sinais que compartilham o espectro eletromagnético. Na figura I acima, ilustra-se, para determinado instante t \ge 0, o circuito de um filtro elétrico composto por uma fonte de tensão v_g, em volts, que representa o sinal de entrada nesse instante, além de dois resistores de resistências R_g e R, um capacitor de capacitância C e uma bobina, que é caracterizada por uma grandeza elétrica denominada indutância (L), cuja unidade é o henry (H).
Considere que, para cada instante t \ge 0, a fonte de tensão seja dada pela função v_g(t) = V_g \text{cos} (\omega t), em que V_g é um número real e \omega \ge 0 é a freqüência angular do sinal de entrada, em rad/s.
Nesse filtro, para cada instante t \ge 0, a tensão elétrica v_R na resistência R é v_R(t) = |V_R| \text{cos} (\omega t + \theta), em que |V_R| e \theta são determinados a partir do número complexo V_R = |V_R| (\text{cos} \theta + i \text{sen} \theta), em que i = \sqrt{-1}.
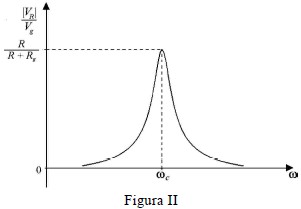
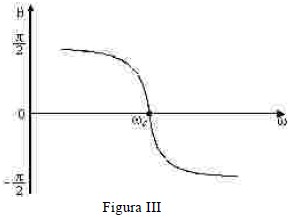
Os gráficos das figuras II e III apresentam, respectivamente, os comportamentos de \large {|V_R| \over V_g} e de \theta, em função de \omega. A freqüência \large \omega_c = {1 \over \sqrt{LC}}, mostrada nas figuras II e III, é denominada freqüência central do filtro e os valores de L e de C devem ser ajustados para que \omega_c coincida com a freqüência do sinal desejado. Note que, na freqüência central, \large {|V_R| \over V_g} é máximo e \theta é nulo.