Abastecimento

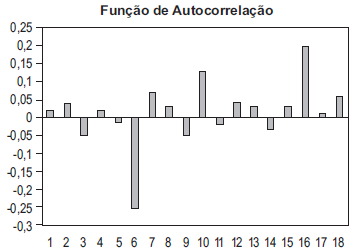
Um analista deseja modelar a evolução de um índice de qualidade de vida e, para isso dispõe de uma série temporal formada por 81 observações mensais. Inicialmente ele tenta ajustar o modelo na forma X_t = \phi X_{t-1} + \varepsilon_t - \theta \varepsilon_{t-1}, em que | \phi | < 1 e | \theta | < 1 são os coeficientes do modelo; X_t é o valor do indicador no mês t; \varepsilon_t representa o ruído branco no mês t com média zero e variância \sigma^2. Abaixo, encontram-se os valores e o gráfico da função de autocorrelação dos resíduos gerados pelo modelo ajustado.

Iag	Função de autocorrelação
1	0,02
2	0,04
3	-0,05
4	0,02
5	-0,01
6	-0,025
7	0,07
8	0,03
9	-0,05
10	0,13
11	-0,02
12	0,04
13	0,03
14	-0,03
15	0,03
16	0,2
17	0,01
18	0,06

A partir desses dados , conclui-se que os resíduos do modelo

seguem o comportamento de um ruído branco.
não seguem o comportamento de um ruído branco, apresentando valor anormal no lag 6.
não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6 e 10.
não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6, 10 e 16.
não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6, 7, 10 e 16.