Enunciados de questões e informações de concursos
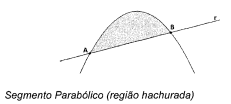
Um dos mais brilhantes trabalhos do matemático grego Arquimedes (287 a.e. - 212 a.C.) foi a Quadratura da Parábola. Através do Método da Exaustão, Arquimedes demonstrou que a área de um segmento parabólico (região compreendida entre a parábola e uma linha reta r), conforme figura abaixo.
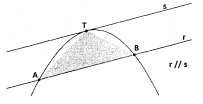
Essa área do segmento parabólico equivale a \frac {4}{3} da área do triângulo ABT seguinte, inscrito no segmento parabólico, sendo as retas r e s paralelas e T o ponto de tangência.
Seja p uma parábola com foco F (- \frac {\sqrt{2}}{2}; \frac{3\sqrt{2}}{2}) e reta diretriz d: x + y +\sqrt{2} = 0.
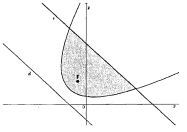
A parábola é seccionada pela reta r: \sqrt{2} . x + \sqrt {2.y} - 8 = 0, originando a região hachurada da figura abaixo.
Com base nas informações apresentadas, é correto afirmar que a área da região hachurada é igual a
Outras questões do mesmo concurso: EN / Asp Of (EN) / 2021
