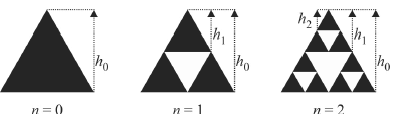
Por permitirem que os smartphones utilizem uma única antena para sinais de GPS, de wi-fi, de bluetooth e outros, as antenas fractais, operando em diversas frequências, são mais versáteis que as comuns. Um modelo de antena fractal, que usa o triângulo de Sierpinski, pode ser construída a partir de uma chapa de metal no formato de um triângulo equilátero de altura h0. Nesse estágio (estágio 0), a antena trabalha em uma frequência f0; aqui { \large f_0 \over h_0} = K. Eliminando-se da chapa de metal o triângulo formado pelos pontos médios dos lados do primeiro triângulo, restam três triângulos de metal, equiláteros e de altura h1. Nesse estágio (estágio 1), a antena continua trabalhando na frequência f0, mas passa a trabalhar também na frequência f1, em que f1 é tal que { \large f_1 \over h_1} = K, e k é a mesma constante do estágio 0. Repetindo sucessivamente o processo de retiradas de triângulos da chapa de metal, incluem-se novas frequências, f2, f3, ..., fn, ..., em que, para cada n, fn é tal que { \large f_n \over h_n} = K , hn é a altura do triângulo equilátero no estágio n, e k é a mesma constante dos estágios anteriores. As figuras a seguir exemplificam os estágios 0, 1 e 2.
Enunciados de questões e informações de concursos
A partir da construção descrita, julgue o item que se segue.
Para construir a antena em qualquer etapa, foi necessário remover triângulos de metal que, juntos, equivalem a { \large 1 \over 4} da área que a antena tinha na etapa anterior.
-
Errado
Outras questões do mesmo concurso: UnB / Vest (UnB) / 2019 / EAD / Licenciatura UAB
Questões comentadas
Questões sem comentário
P1 - Prova Objetiva

Ocorreu um erro na requisição, tente executar a operação novamente.