Considerando que um auditor fiscal encarregado de analisar indícios de irregularidades em obras de um determinado estado tenha analisado 50 obras e constatado irregularidades em 40 delas, julgue os itens a seguir.
107 O desvio padrão da amostra foi inferior a 0,05.
Resolução:
Nesta questão cabe recurso!
Pergunta básica: afinal de contas, qual é a variável aleatória que estamos analisando?
Não sei, a banca não definiu.
Uai, se não sabemos sequer que variável está sendo analisada, como é que vamos calcular desvio padrão de alguma coisa? Desvio padrão do quê???
Sugestão de redação:
A questão, em momento algum, define qual a variável aleatória em estudo. Não se sabe se é a probabilidade de irregularidade a cada extração (a cada obra analisada), se é o número de obras irregulares na amostra, se é o valor da obra, ou se é qualquer outra grandeza.
A definição exata da grandeza em estudo é crucial para a resolução da questão. Sem esta informação, pede-se a sua anulação.
Em todo caso, supondo que a cada obra analisada a gente defina uma variável de Bernoulli de parâmetro "p", e indicando 1 em caso de irregularidade e 0 em caso de regularidade, a proporção amostral observada seria de:
hat p = {40 over 50} = 0,8
O desvio padrão amostral é assim calculado:
sqrt {hat p times (1- hat p over n} = sqrt {0,8 times 0,2 over 50}
={0,4 over sqrt {50}} = {0,4 times sqrt {50} over 50}
Vamos aproximar a raiz de 50 como 7:
approx 0,056
Item errado.
108 Se o total de obras, nesse estado, for igual a 300, então o fator de correção para a população finita deverá ser maior que 0,8.
Resolução.
Fórmula do fator:
{N - n over N-1}
Em que N é o tamanho da população e "n" é o tamanho da amostra:
={300-50 over 300-1} approx 0,83
Item certo
Obs: mesmo que o examinador estivesse se referindo ao fator de correção para o desvio padrão, que corresponderia à raiz de 0,83, a resposta ainda seria "certo". Isso porque a raiz de 0,83 é maior que 0,83. Esta é uma propriedade dos números no intervalo entre 0 e 1. Quando tiramos a raiz quadrada, o resultado aumenta.
109 Mais de 70% das obras auditadas apresentaram irregularidades
Resolução:
O percentual de obras com irregularidades é de 80%, conforme calculamos no item 107. Item certo.
Um auditor foi convocado para verificar se o valor de Y, doado para a campanha de determinado candidato, estava relacionado ao valor de X, referente a contratos firmados após a sua eleição.
Com base na situação hipotética e na tabela apresentadas, julgue os itens que se seguem, considerando-se que
sum (X_i - bar X)^2=17,5
E(Y^2)=7,25
110 A média de Y (valor doado para a campanha) é maior que 2.
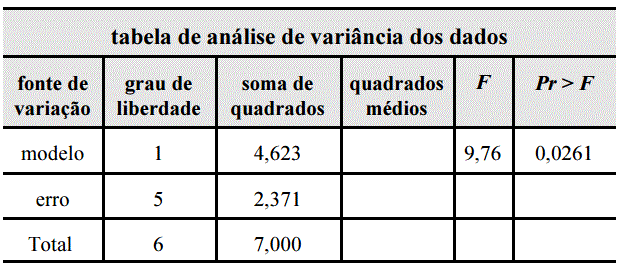
Se são 6 graus de liberdade ao todo, então são 7 observações (basta somar 1).
n=7
A esperança do quadrado de Y vale 7,5:
{sum Y^2 over 7} = 7,25
A soma de quadrados total fica:
sum (Y - overline Y)^2 = 7
sum Y^2 - n times overline Y^2 = 7
Dividindo todos os termos por 7:
7,25- overline Y ^2 = 1
overline Y ^2 = 6,25
overline Y = 2,5
Item certo.
111 O modelo em questão apresenta ajuste inferior a 0,5.
Basta dividir a soma de quadrados do modelo pela soma de quadrados total:
{4,623 over 7} approx 0,66
Item errado.
112 O coeficiente angular é maior que 1.
Vamos partir da definição da soma de quadrados do modelo de regressão (SQM):
SQM = sum (hat Y - bar Y)^2
SQM = sum (a+bX - bar Y)^2
O coeficiente linear é dado por bar Y - bbar X
SQM = sum (bar Y - b bar X +bX- bar Y)^2
SQM = b^2 times sum (X- bar X)^2
É claro que o candidato não precisaria fazer esse passo a passo todo, desde que já soubesse direto a fórmula acima.
4,623=b^2times 17,5
b^2 approx 0,264
O que nos mostra que b^2 < 1 to b < 1. Item errado.
113 O valor da estatística t para o coeficiente angular é maior que 3.
Resolução:
A estatística "t" é a raiz quadrada da estatística F.
t= sqrt {9,76}
Que de fato é maior que 3.
ITEM CERTO.